Der Schildkrötenbaum #
Selbstähnlichkeit #
Kennst du den schon?
Wofür steht das »B« in Benoit B. Mandelbrot?
Benoit Mandelbrot hat der Welt ein Geschenk hinterlassen: fraktale Geometrie. Selbstähnlichkeit spielt dabei eine Rolle, und die lässt sich prima mit Rekursion fassen.
Findest du in diesem Bild Formen, die sich ähnlich sind?
Die Frage ist nicht schwer – die Quadrate sind zwar unterschiedlich groß, doch sich ansonsten selbst ähnlich.
Eine solche Figur lässt sich unproblematisch von einer Schildkröte zeichnen:
import turtle
def quadrat(schildkroete, laenge):
schildkroete.down()
for _ in range(4):
schildkroete.forward(laenge)
schildkroete.left(90)
schildkroete.up()
turti = turtle.Turtle()
quadrat(turti, 100)
turti.fd(120)
quadrat(turti, 87)
turti.fd(107)
quadrat(turti, 50)
Die Funktion quadrat nimmt neben der Länge ein Schildkröten-Objekt entgegen, und zeichnet ein Quadrat mit der ebenfalls übergebenen Seitenlänge.
Schildkröten-Objekt?
Was Objekt in diesem Zusammenhang übrigens genau bedeutet, schauen wir uns im nächsten Level an. Vielleicht kannst du dir aber denken, was passiert: die Schildkröte, die eben noch
turtihieß, wird der Funktion übergeben, und ist nun in ihr mit dem Namenschildkroeteansprechbar.
Nun lassen sich diese drei Quadrate auch interessanter anordnen:
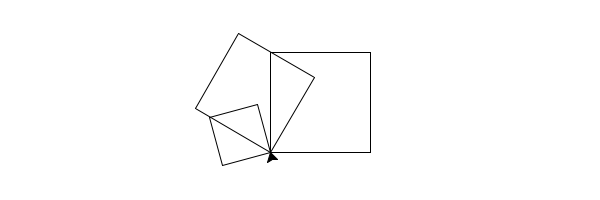
turti = turtle.Turtle()
quadrat(turti, 100)
turti.left(60)
quadrat(turti, 87)
turti.left(45)
quadrat(turti, 50)
Versuche es selbst! Ordne die Quadrate auf interessante Weise an!
Der Baum des Pythagoras #
Vielleicht ist dir aufgefallen, dass sich auch dies mit den drei Quadraten anfangen lässt:
import turtle
def quadrat(schildkroete, laenge):
schildkroete.down()
for _ in range(4):
schildkroete.forward(laenge)
schildkroete.left(90)
schildkroete.up()
# Schildkröte und erstes Quadrat
turti = turtle.Turtle()
quadrat(turti, 100)
# gehe zur linken oberen Ecke
turti.left(90)
turti.fd(100)
# nächstes Quadrat
turti.right(60)
quadrat(turti, 87)
# gehe zur rechten unteren Ecke des neuen Quadrats
turti.fd(87)
#nächstes Quadrat
turti.right(90)
quadrat(turti, 50)
Herauskommen sollte etwas, das du vielleicht noch aus dem Matheunterricht an der Schule kennst: ein rechtwinkliges Dreieck, dessen Seiten gleichzeitig Seiten von Quadraten sind.
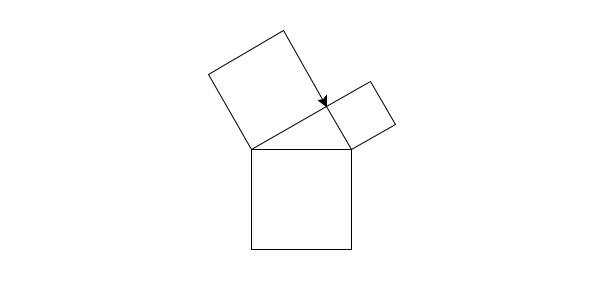
Vielleicht erinnerst du dich auch noch an den Satz des Pythagoras: die Fläche des großen Quadrates ist genau so groß wie die der beiden kleineren zusammen.
Der Baum des Pythagoras macht sich dies zu Nutze: er besteht aus einem Stamm (einem Quadrat), auf dem ein rechtwinkliges Dreieck liegt. Dessen beide (kleinere) Seiten sind wiederum die Basis für Äste (kleinere Quadrate), von denen sich erneut Äste verzweigen.
Wir müssen es also hinbekommen, unserer Turtle eine einzige Figur (aus Quadrat und Dreieck zusammengesetzt) beizubringen. Dann können wir diese rekursiv aufrufen, und dem Baum steht nichts mehr im Wege!
import turtle
def ast(schildkroete, seitenlaenge):
# Proportionen für das rechtwinklige Dreieck
seite_a = seitenlaenge * .866
seite_b = seitenlaenge * .5
# Ast und Basis für neue Äste
schildkroete.left(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(60)
schildkroete.forward(seite_a)
schildkroete.right(90)
schildkroete.forward(seite_b)
schildkroete.right(30)
schildkroete.forward(seitenlaenge)
# Schildkröte geht zurück zum Ausgangspunkt
schildkroete.up()
schildkroete.right(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(180)
if __name__ == '__main__':
turti = turtle.Turtle()
ast(turti, 100)
Gleitkommazahlen
Hier findest du die Schreibweise
.866und.5. Beide Ausdrücke stehen für Gleitkommazahlen.Warum sehen die so merkwürdig aus? Wir schreiben Gleitkommazahlen mit einem Punkt (
.) statt einem Komma – anders würde Python solche Zahlen mit Tupeln verwechseln. Außerdem dürfen wir bei Werten unter1die führende 0 weglassen: schreiben also.5statt0.5.
Und das haben wir davon:
Nun müssen wir lediglich an zwei Stellen rekursiv Äste anhängen, um einen Baum zu bekommen. Oder?
import turtle
def ast(schildkroete, seitenlaenge):
# Proportionen für das rechtwinklige Dreieck
seite_a = seitenlaenge * .866
seite_b = seitenlaenge * .5
# Ast und Basis für neue Äste
schildkroete.left(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(60)
# Erster rekursiver Aufruf
ast(schildkroete, seite_a)
schildkroete.forward(seite_a)
schildkroete.right(90)
# Zweiter rekursiver Aufruf
ast(schildkroete, seite_b)
schildkroete.forward(seite_b)
schildkroete.right(30)
schildkroete.forward(seitenlaenge)
# Schildkröte geht zurück zum Ausgangspunkt
schildkroete.up()
schildkroete.right(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(180)
if __name__ == '__main__':
turti = turtle.Turtle()
ast(turti, 100)
Doch was ist das? Anstatt vollständiger Figuren sehen wir nur eine Spirale!
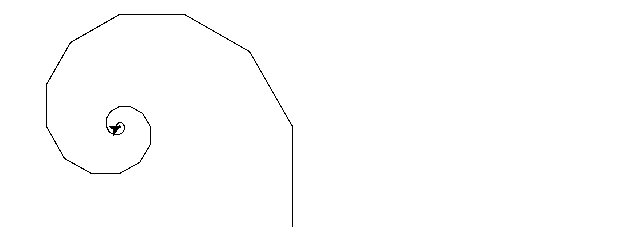
Im Moment ruft die Funktion für jeden Funktionsaufruf einmal sich selbst auf, und zwar, bevor sie selbst beendet ist – das kann also gar nicht anders gehen!
Damit wir den Baum irgendwann einmal fertig bekommen, sollten wir die Tiefe der rekursiven Aufrufe kontrollieren. Dazu können wir eine künstliche Rekursionsvariable verwenden. Wir übergeben die Variable neben Schildkröte und Länge:
def ast(schildkroete, seitenlaenge, tiefe):
# …
Und verringern mit jedem rekursiven Aufruf die Tiefe um eins. Ist die Tiefe erreicht, ist tritt der Basisfall ein, und der rekursive Aufruf findet nicht mehr statt.
# Erster rekursiver Aufruf
if tiefe > 0:
ast(schildkroete, seite_a, tiefe-1)
Ebenso beim zweiten rekursiven Aufruf:
# Zweiter rekursiver Aufruf
if tiefe > 0:
ast(schildkroete, seite_b, tiefe-1)
Eine letzte Zeile ist noch wichtig. Damit die Schildkröte weitermalen kann, muss sie nach Erreichen des Ausgangspunktes den Stift wieder senken. Ganz zum Schluss der Funktion fehlt also noch:
schildkroete.down()
Um zu starten, rufe die Funktion ast mit gewünschter Tiefe auf, z.B. so:
if __name__ == '__main__':
turti = turtle.Turtle()
ast(turti, 100, 9)
Dann sollte sich, nach einigem Warten, dieses Bild ergeben:
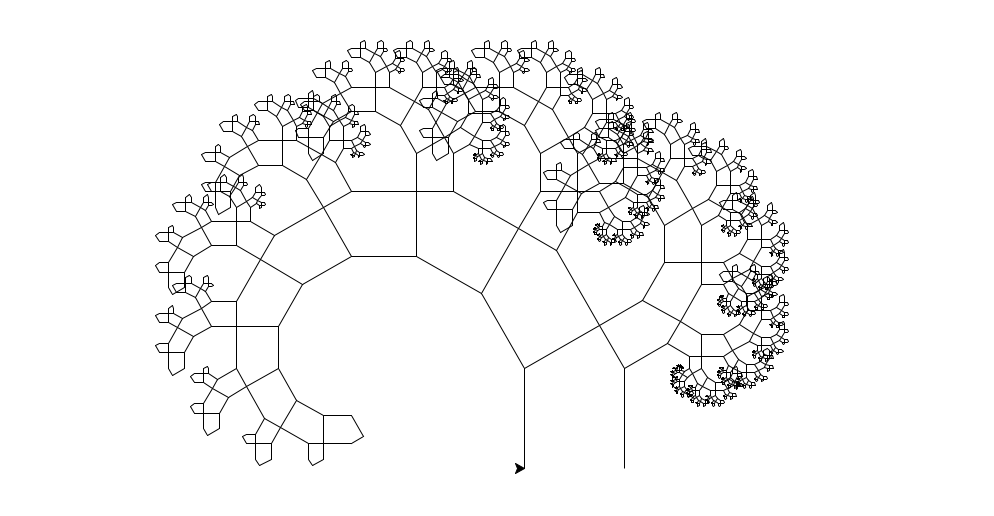
Im ganzen sieht unser Code nun so aus:
import turtle
def ast(schildkroete, seitenlaenge, tiefe):
# Proportionen für das rechtwinklige Dreieck
seite_a = seitenlaenge * .866
seite_b = seitenlaenge * .5
# Ast und Basis für neue Äste
schildkroete.left(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(60)
# Erster rekursiver Aufruf
if tiefe > 0:
ast(schildkroete, seite_a, tiefe-1)
schildkroete.forward(seite_a)
schildkroete.right(90)
# Zweiter rekursiver Aufruf
if tiefe > 0:
ast(schildkroete, seite_b, tiefe-1)
schildkroete.forward(seite_b)
schildkroete.right(30)
schildkroete.forward(seitenlaenge)
# Schildkröte geht zurück zum Ausgangspunkt
schildkroete.up()
schildkroete.right(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(180)
schildkroete.down() # Damit weitergemalt werden kann
if __name__ == '__main__':
turti = turtle.Turtle()
ast(turti, 100, 9)
Wenn du nun findest, so ein unbelaubter Baum sieht doch sehr nach einem trüben Wintertag aus: du hast Recht! Wie wäre es mit dieser Frühlingsversion? Einige wenige Änderungen, und schon blühen die Schildkröten am Schildkrötenbaum!
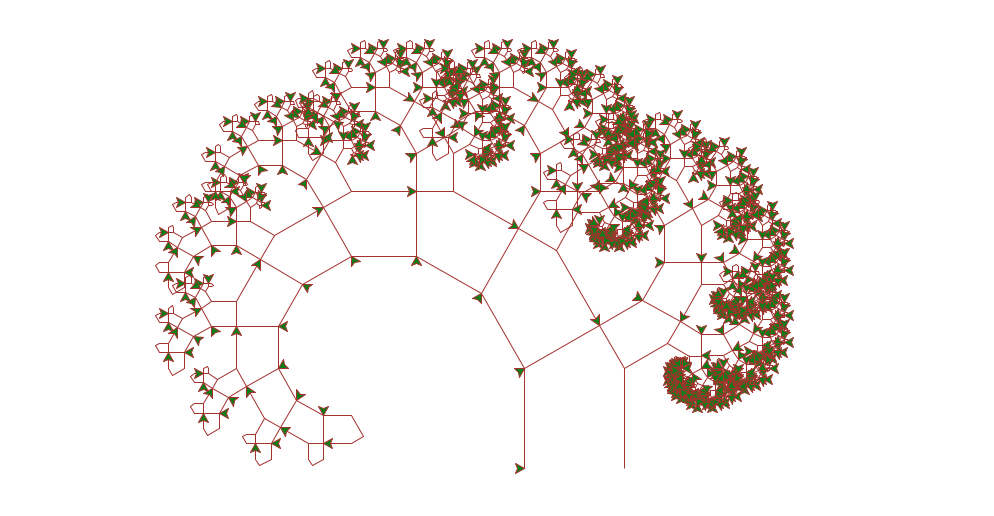
import turtle
def ast(schildkroete, seitenlaenge, tiefe):
# Proportionen für das rechtwinklige Dreieck
seite_a = seitenlaenge * .866
seite_b = seitenlaenge * .5
# Ast und Basis für neue Äste
schildkroete.left(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(60)
# Erster rekursiver Aufruf
if tiefe > 0:
ast(schildkroete.clone(), seite_a, tiefe-1)
schildkroete.forward(seite_a)
schildkroete.right(90)
# Zweiter rekursiver Aufruf
if tiefe > 0:
ast(schildkroete.clone() , seite_b, tiefe-1)
schildkroete.forward(seite_b)
schildkroete.right(30)
schildkroete.forward(seitenlaenge)
# Schildkröte geht zurück zum Ausgangspunkt
schildkroete.up()
schildkroete.right(90)
schildkroete.forward(seitenlaenge)
schildkroete.right(180)
schildkroete.down()
if __name__ == '__main__':
turti = turtle.Turtle()
turti.speed(0)
turti.color('brown', 'green')
ast(turti, 100, 9)



